There has been growing interest relating Causal Inference (CI) to Reinforcement Learning (RL). While there are some great achievements in solving high dimensional RL problems, research on the intersection of RL and CI is still in its diapers. What makes these problems hard, and how do they relate to RL? In this blog we’ll give our view.
If you’re new to Causal Inference, this blog post is a great place to start. If you want to dive even deeper, check out one of Jeuda Pearl’s books on Causal Inference.
Let’s start with a very basic question: Do we have CI related problems in RL? If we have a simulator of some fully observable Markov decision process, then we already have the causal diagram of the world, right? Then, we can always ask statistical questions such as:
- Was a given action the cause of us receiving high reward?
- Which action/s in the past were the consequential cause of us reaching some state (this is tightly related to the so-called “temporal credit assignment problem״)?
- What would have happened if we were to take a different action than that we actually took (counterfactual analysis)?
These types of questions can theoretically be estimated from observations without the need of tools from CI. So again… where does CI meet RL?
There are several reasons CI is important for RL. In this blog post we will only focus on one aspect: offline RL (a.k.a batch RL). The use of off-policy batch data is a hard problem on its own. Nevertheless, it is many times unavoidable. The most prominent setting where this is evident is the medical domain. There, an abundance of data is readily available, while simulators are either unavailable or inaccurate. Moreover, real-world experiments are long, expensive, full of bureaucracy, and many times simply impossible or unethical to conduct.
Okay… So we are stuck with some offline off-policy data (perhaps even much of it), and the question of “what is a good policy?”. How can we make best use of this data?
The use of off-policy offline data in RL is usually inefficient, making the problem hard to begin with. In many settings, such data is not even created by us (the designers). This means that some other agent, who some of us like to call the behavioral agent, chose actions according to his/her own beliefs. We do not control the agent’s behavioral policy. This makes it difficult (or even impossible) to estimate what would happen in certain states, where our observations are scarce to non-existent. There has been much work attempting to solve the offline-RL problem, from estimating Important Sampling ratios, to off-policy evaluation, through policy improvement and doubly robust estimates.
So hopefully you’re convinced off-policy offline RL is important and hard. Let’s make it a little bit harder. We already said that we don’t know the behavioral policy that generated the data. But in fact, we don’t even know the behavioral agent’s full state of information. This means that our data does not necessarily hold all observations that were the cause of the behavioral agent’s choices. These are also known as unobserved confounders in the CI literature. Mathematically, the behavior policy may be a mapping from states to actions, but in our data we only get to see noisy observations of these states. For example, the age or sex of a patient may be a decisive factor in determining how to treat this patient. Such information may not be revealed to the us.
If we don’t get to see the real states in our data, how can we get unbiased estimates of the value of a policy different from the behavioral policy, a policy we call the evaluation (or target) policy? One approach would attempt to simply ignore this fact. But this would usually be a bad idea, as it could lead to disastrous conclusions, such as prescribing a patient with a completely wrong treatment. Let’s show this with a very simple example.
Consider the following two state problem:
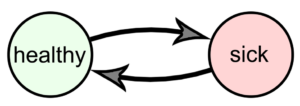
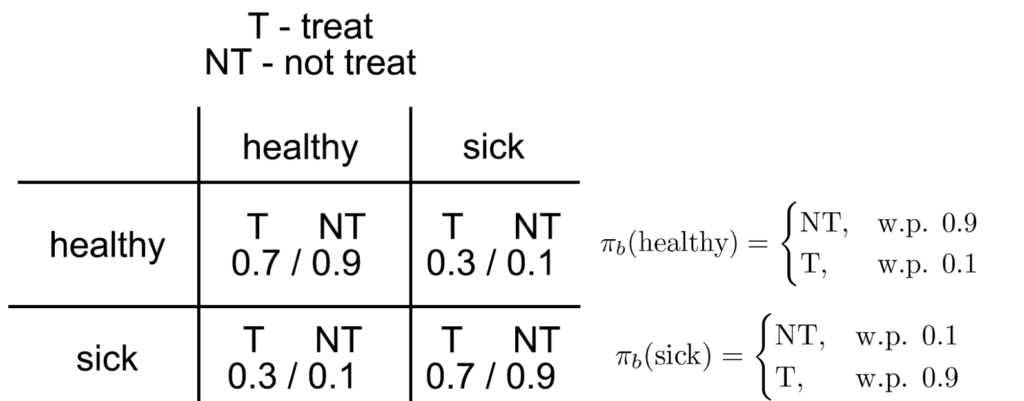
We will give an agent a reward of -1 for being sick and a reward of 0 for being healthy. We will also assume that we always start healthy with probability 1. Now, assume we have data generated by the above process. To make the point as clear as possible, let’s assume we have access to an infinite amount of this data. This means we can evaluate exactly any policy using (for example) the Importance Sampling method:
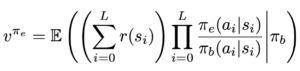
What would happen if what we saw in our data wasn’t the real state, but rather some noisy observation of it? Say for example our data consists of observations of the state of the sort:
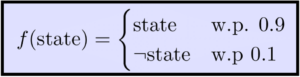
If we only get to see such noisy observation of the state, then using the naive estimator above would yield
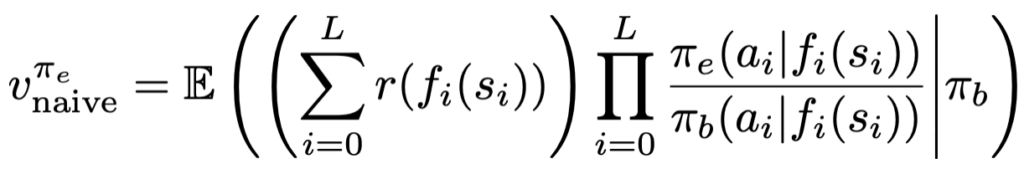
Note that we are still using an infinite amount of data, but the estimator we got is statistically biased. Actually, this bias grows with the horizon, as you can see in the plot below:
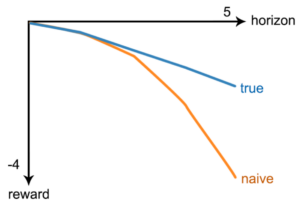
These types biases exist in real offline data. Going back to our initial question: do we have a causal problem in RL? The answer is yes, anytime we wish to make use of offline off-policy data. The fact that an MDP readily gives us the causal structure of the world may be true. The problem is we don’t have access to the real MDP, nor do we know what the real MDP is. Answering any counterfactual question must come with the realization that significant biases could be built into our data through confounding effects of spurious or distorted associations. CI makes us aware of possible unobserved variables (confounders) that can give rise to such biases. It lets us rigorously reason about confounding. While it is not always possible to eliminate them, we can mitigate these biases, bringing them to a minimum, thereby grounding our conclusions with reality.