Lior Shani*, Yonathan Efroni* and Shie Mannor
Published at ICML 2019
Paper, Code
What?
We analyze optimization criteria that are aware of the exploration policy and propose Exploration-Conscious converging versions for DQN (Q-Learning) and DDPG.
Author: Lior Shani @liorshan
Why?
Most empirical works use some fixed exploration scheme [1,2,3,4]. This exploration scheme is usually a predefined perturbation to the agent’s decisions, which forces it to try less explored actions every now and then. For discrete action spaces, usually \(\epsilon\)-greedy exploration is used, and for continuous action spaces, the most common choice is adding a Gaussian noise with standard deviation \(\sigma\) around the chosen action.
Thus, unfortunately, when an agent tries to explore, it does not use any knowledge he might already possess regarding the outcome of the explored action.
Imagine this robot-guy, learning how to take amazing selfies using a fixed exploration scheme.
In order to learn, he must explore.

However, exploration might cause him to fall off the cliff, in many different learning episodes. In turn, this can lead to poor learning, as the episode terminates when he falls, and he is no longer able to acquire new experiences.

Instead, we consider in our work Exploration-Conscious reinforcement learning. Being Exploration-Conscious means that the agent is “aware” that he might explore due to the fixed exploration scheme.
This causes the agent to learn policies which prevents the hazards caused by exploration.
In our work, we analyze Exploration-Conscious learning criteria, and offer algorithms to solve them.

How?
The goal of RL agents is to find the policy which maximizes the expected discounted rewards. This goal can be described in the following optimization problem:
\(\pi^* \in \arg\max_{\pi’\in \Pi} {\mathbb{E}}^{\pi’} \left[\sum_{t=0} \gamma^t r(s_t,a_t)) \right]\)
Value iteration inspired algorithms such as Q-learning, use the Bellman equation to find the optimal value [5]:
\(v(s) = max_a r(s,a) + \gamma \sum_s’ p(s’|s,a) v(s’)\)
Thus, the TD update rule for Q-learning with learning rate \(\eta_t\) is:
\(Q(s_t,a_t) = Q(s_t,a_t) + \eta_t (r_t + \gamma \max_a Q(s_{t+1},a) – Q(s_t,a_t)\)
Notice that the value of the next state is replaced by \(\max_a Q(s_{t+1},a)\), which is an estimation of the value we get by following the greedy policy which maximizes the Q-function estimate of the next state \(s’\).
Nonetheless, we know in advance that while the agent is still training, he might explore in the future. In other words, while training, the agent does not follow the greedy policy. Instead, it follows the predefined fixed exploration scheme: For example, using \(\epsilon\)-greedy exploration, with probability \((1-\epsilon)\) the agent follows the greedy policy, yet with probability \(\epsilon\) it follows the uniform policy over all actions, which we denote by \(\pi_0\).
As a result, we consider in our work an alternative goal:
Find a policy which maximizes the expected rewards when using exploration
This goal can be written as the following optimization problem:
\(\pi^*_{\epsilon} \in \arg\max_{\pi’\in \Pi} {\mathbb{E}}^{\pi^\epsilon(\pi’,\pi_0)} \left[\sum_{t=0} \gamma^t r(s_t,a_t)) \right]\),
Where \(\pi^\epsilon(\pi’,\pi_0)\) is a convex mixture between the greedy policy and the \(\pi_0\) , i.e., \(\pi^\epsilon(\pi’,\pi_0) = (1-\epsilon)\pi’ + \epsilon \pi_0\). We call this objective the Exploration-Conscious RL criterion.
The resulting optimization problem is a constrained optimization problem, where we look for the best policy in the set of policies which fits the predefined exploration scheme.
The key insight of our work is that we can solve this constrained optimization problem by looking at it from another perspective: By thinking of the exploration noise as a perturbation caused by the environment. In other words, we define a new surrogate MDP, which includes the noise caused by exploration.
For example, in the case of $\epsilon$-greedy exploration we define the following surrogate MDP:
\(r_\alpha(s,a) = (1-\epsilon) r(s,a) + \epsilon \sum_a \pi(a|s) r(s,a)\) \(P_\alpha(s’\mid s,a) = (1-\epsilon) P(s’\mid s,a) + \epsilon \sum_a \pi(a|s) P(s’\mid s,a)\)
As we already know how to solve MDPs, we can solve the surrogate MDP to find the solution of the Exploration-Conscios RL optimization problem. This intuition is formally proved in our paper.
Performance of Exploration-Conscious Criteria
When an agent is Exploration-Conscious, it tries to act optimally on the surrogate MDP. In other words, the agent tries to learn how to act optimally while training, i.e., when exploration is employed. However, when evaluating the agent’s policy, it is reasonable to expect that the optimal Exploration-Conscious policy will not perform as good as the optimal policy.
On the other hand, by using Exploration-Conscious RL we restrict the policy class. Thus, it might be easier to learn the optimal policy. For example, consider the case where \(\epsilon=1\). Indeed, for any \(\pi’\),
\(\pi^\epsilon(\pi’,\pi_0) = (1-\epsilon)\pi’ + \epsilon \pi_0 = \pi_0\),
Which means that every policy is optimal!
In the paper, we formalize this bias-error sensitivity tradeoff: while optimizing Exploration-Conscious criteria adds bias to the problem, it also becomes easier to solve.
Algorithms
Observe that in each iteration, we gather information using the following process:
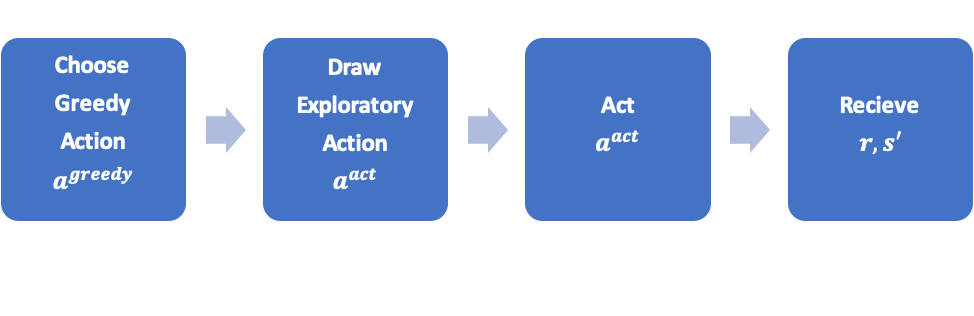
Regular RL algorithms make use of the following information tuple \(\langle s,a^{\text{act}},r,s’\rangle\).
However, being aware to the exploration process we actually obtain the following information tuple \(\langle s,a^{\text{greedy}},a^{\text{act}},r,s’\rangle\).
This understanding allows us to devise two different approaches to solve the Exploration-Conscious criteria. In the paper, we show how these two approaches can be implemented on top of Q-Learning [5] for solving MDPs with discrete action spaces, and on top of DDPG [1] for continuous action spaces.
Expected approach
1. Update \(Q^{\pi^\alpha}(s_t,a_t^{\text{act}})\) 2. Expect that the agent might explore in the next state:
\(Q^{\pi^\alpha}(s_t,a_t^{\text{act}}) = Q^{\pi^\alpha}(s_t,a_t^{\text{act}}) + \eta(r_t + \gamma \mathbb{E}^{a\sim (1-\alpha)\pi+\alpha \pi_0}Q^{\pi^\alpha}(s_{t+1},a) – Q^{\pi^\alpha}(s_t,a_t^{\text{act}})\)
This approach solves the Exploration-Conscious problem directly.
Notice that this approach requires to calculate expectations. This requires sampling to compute both the values and gradients, when the action space is continuous.
Thus, we offer another take on how to solve the Exploration-Conscious problem – the surrogate approach.
Surrogate approach
1. Update \(Q^{\pi^\alpha}(s_t,a_t^{\text{greedy}})\) 2. The rewards and next state \(r_t,s_{t+1}\) are given by the taken action \(a_t^{\text{act}}\)
\(Q^{\pi^\alpha}(s_t,a_t^{\text{greedy}}) = Q^{\pi^\alpha}(s_t,a_t^{\text{greedy}}) + \eta(r_t + \gamma Q^{\pi^\alpha}(s_{t+1},a_{t+1}^{\text{greedy}}) – Q^{\pi^\alpha}(s_t,a_t^{\text{greedy}})\)
Here, we solve the surrogate MDP, which means that the exploration is incorporated into the environment.
In this approach there is no need for sampling, which makes it easier to use when dealing with continuous action-spaces.
The full deep RL variants of the proposed algorithms are described here:


Experiments
We test the two approaches on a subset of Atari 2600 games, and on a set of MuJoCo continuous control tasks. We have chosen the games to fit the logic of being exploration-conscious. For example, in Qbert, the agent can jump off the cliff due to the exploration, as in the cliff walking given in the beginning of this blog.
As the table shows, our method surpasses the baselines algorithm in both cases.
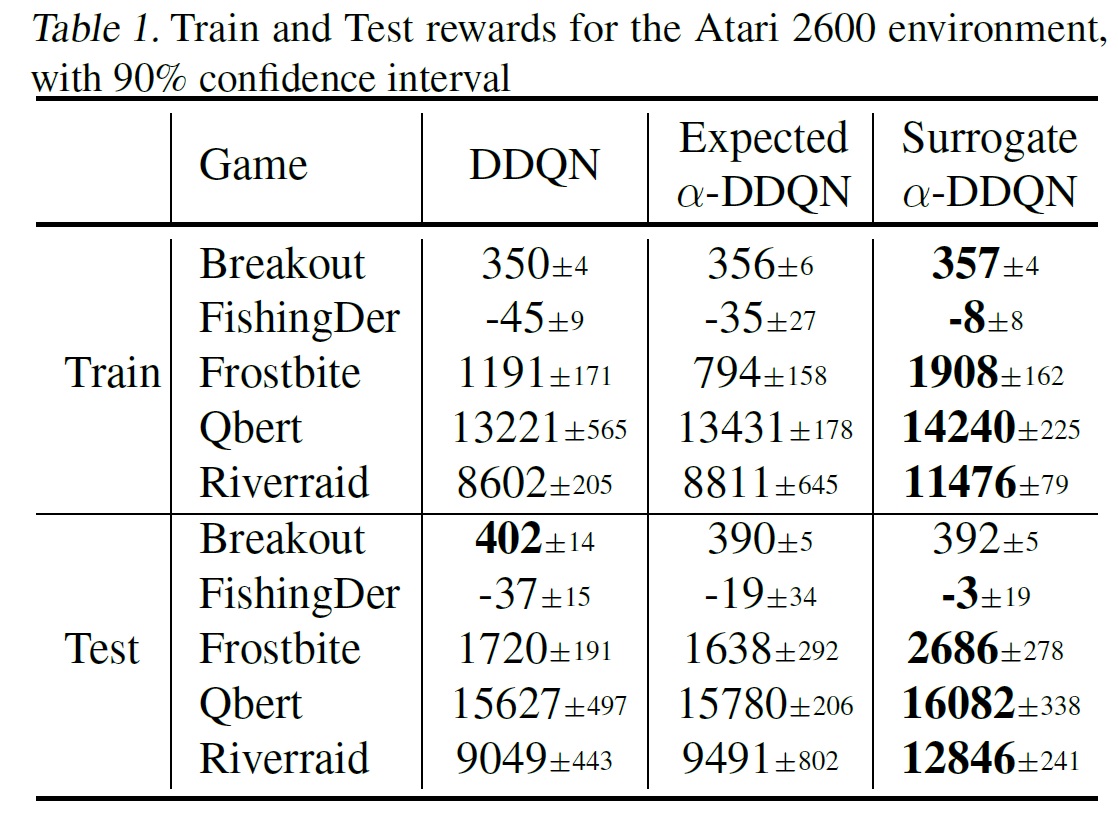
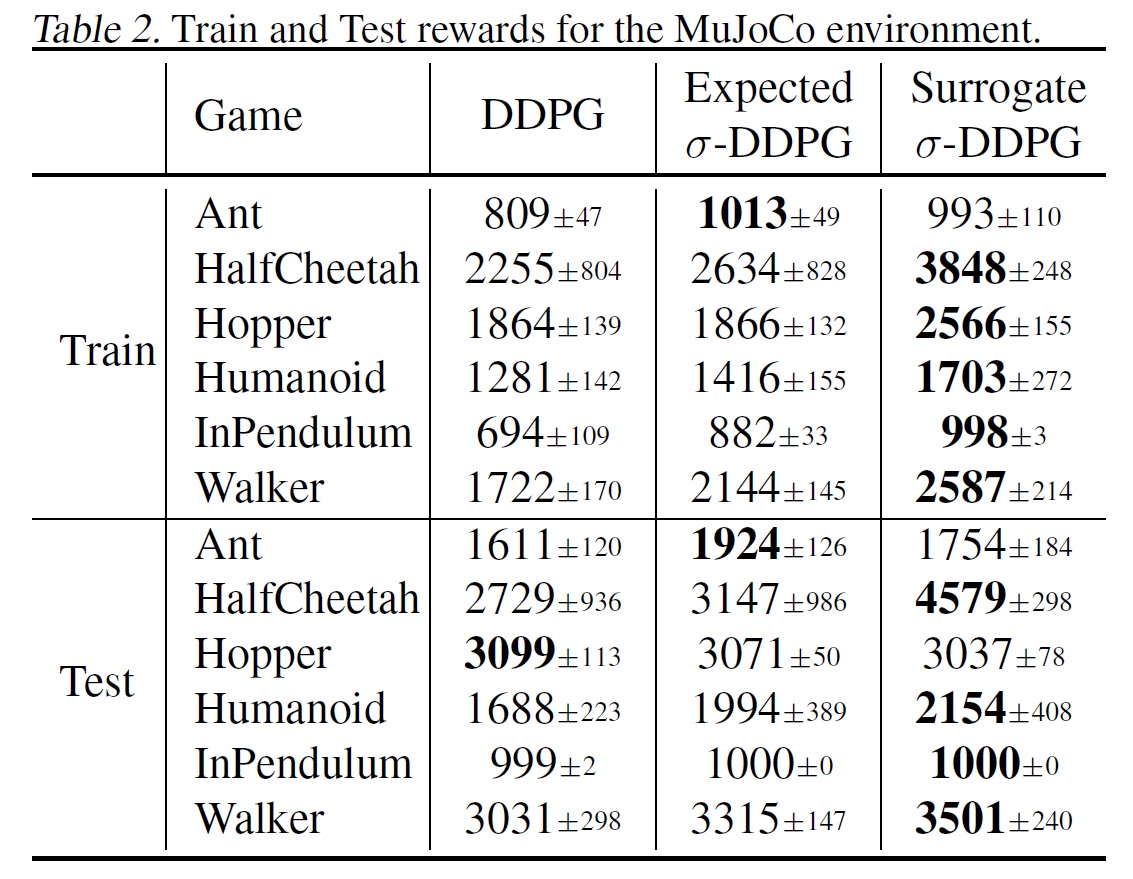
When training, the agent explores using the fixed exploration scheme. Indeed, using the exploration-conscious algorithms, we solve the surrogate MDP, which is the exactly the MDP used in training regime. Thus, there is no surprise that the agent performs better in this setting.
More importantly, the exploration-conscious variants also perform better than their vanilla counter parts in the test regime, i.e., when evaluating the learned policy without applying any exploration. Thus, the results justify the use of exploration-conscious RL algorithms, which follows the following reasoning:
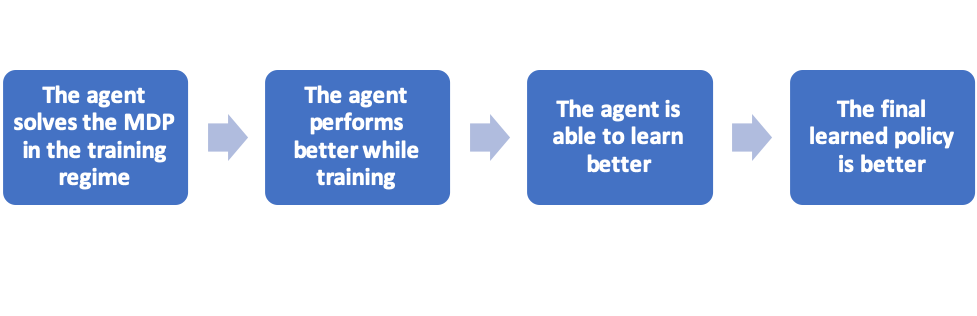
While the optimal exploration-conscious policy can be biased with respect to the optimal policy, in complex problems, we are usually satisfied with a good enough solution. In these cases, it is worth considering exploration-conscious RL, as it allows for a better training process.
Interestingly, the surrogate approach proves superior in most cases: for continuous control tasks, a plausible explanation might be that there is no need to sample, which makes the learning easier and more stable. In the general case, we attribute this to the fact that the implementation of Surrogate \(\alpha\)-DDQN version is somewhat easier than its Expected \(\alpha\)-DDQN counterpart.
Conclusions
• Exploration-Conscious RL admit a bias-error sensitivity tradeoff:
the exploration-conscious solution might not be as good as the optimal one, but it is easier to learn.
• Exploration-Conscious RL can improve performance over both the training and evaluation regimes.
• The novel Surrogate approach requires less computation and produces better results.
• Exploration-Conscious RL can easily help to improve variety of RL algorithms.
Bibliography
[1] Silver, D., Lever, G., Heess, N., Degris, T., Wierstra, D., and Riedmiller, M. Deterministic policy gradient algorithms. In ICML, 2014..[2] Schulman, J., Wolski, F., Dhariwal, P., Radford, A., and Klimov, O. Proximal policy optimization algorithms. arXiv preprint arXiv:1707.06347, 2017.
[3] Mnih, V., Kavukcuoglu, K., Silver, D., Rusu, A. A., Veness, J., Bellemare, M. G., Graves, A., Riedmiller, M., Fidjeland, A. K., Ostrovski, G., et al. Human-level control through deep reinforcement learning. Nature, 518(7540): 529, 2015
[4] Mnih, V., Badia, A. P., Mirza, M., Graves, A., Lillicrap, T., Harley, T., Silver, D., and Kavukcuoglu, K. Asynchronous methods for deep reinforcement learning. In International Conference on Machine Learning, pp. 1928– 1937, 2016.
[5] Sutton, R. S., Barto, A. G., et al. Reinforcement learning: An introduction. MIT press, 1998.